Michael Rüsing

B. M. V. - Schule, Bardelebenstraße 9, 45147 Essen
Kontakt: michael@ruesing-essen.de

Ich unterrichte in der Klasse 11g an der B.M.V. Schule in Essen mit 24 Schülerinnen zum ersten Mal nach dem neuen Lehrplan in der Sekundarstufe II. Den Versuch, den neuen Lehrplan in dieser Klasse umzusetzen, stelle ich in diesem Erfahrungsbericht dar.

Bei der Lektüre des neuen Lehrplanes bin ich schnell auf die Bemerkung gestoßen: "ein anschaulich geprägter und nicht-formaler Grenzwertbegriff reicht an dieser Stelle völlig aus". Mich interessierte, wie weit bei meinen Schülerinnen ein solcher anschaulich geprägter Grenzwertbegriff beim Eintritt in die Oberstufe bereits vorhanden war. Deshalb habe ich beschlossen, das zu Beginn des Unterrichtes in der Klasse 11 auszuprobieren, und mit dem Thema "Grenzwert" begonnen.

Als Einstieg wählte ich das Paradoxon des Zenon. In diesem Zusammenhang wurden einige weitere Aufgaben bearbeitet. Für die Eigenschaft "immer dichter herankommen" wurde ganz zwanglos der Begriff Grenzwert und die zugehörige Schreibweise verwendet.

Gleichzeitig stellte ich den Schülerinnen die Frage, einmal nachzudenken, wo sie derartiges in der Sekundarstufe I schon kennengelernt hatten. Ergebnis: Fehlanzeige! Ich mußte entsprechende Stellen nennen: Dezimalbrüche, Intervallschachtelung, Kreisfläche. Eine Zeit lang hielten wir uns bei den Dezimalbrüchen auf und kamen dabei auf das Problem von 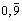. Die Vorstellungen der Schülerinnen waren sehr interessant für die Frage nach der Grenzwertvorstellung. 

Zur Berechnung von Grenzwerten wurden schließlich die Grenzwertsätze ohne Beweis benutzt.

Nach den Grenzwertuntersuchungen habe ich die Themen "Modellierung" und "Koordinatengeometrie" behandelt. In diesem Teil des Unterrichts wurden bereits Grundlagen für die Analysis gelegt, dadurch dass von Anstiegsraten oder Änderungsraten gesprochen wurde. Es kamen auch bereits an dieser Stelle Fragen, wie den die Änderungsrate bei nicht linearem Verlauf des Graphen bestimmt werden könnte. Das Eingehen auf diese Fragen, das sofort zum Ableitungsbegriff geführt hätte, wäre hier schon möglich gewesen. Das wurde leider durch den Klausurtermin verhindert. Die Schülerinnen mußten auf später vertröstet werden.

Zur eigenständigen Vorbereitung auf die 1. Klausur gestalteten die Schülerinnen eigene Übungsaufgaben. Diese Aufgaben zeigen die Inhalte des Unterrichts zu diesen Themen. Die Schülerinnen formulierten zum Teil komplexere Aufgabenstellungen, als sie im Unterricht vorgekommen waren.

Nach der  Klausur bot es sich an, zunächst mit der Koordinatengeometrie fortzufahren, da der Abstand zur 2. Klausur Klausuren äußerst kurz war. Dabei wurden Geraden- und Parabelgleichungen wiederholt und in konkreten Situationen angewendet. Speziell die  Parabeln wurden im Zusammenhang mit Brücken und Satellitenantennen betrachtet. Kreise wurden nur kurz betrachtet unter der Fragestellung, warum denn Satellitenantennen nicht aus Kugelteilen hergestellt werden.

Erst nach diesem Abschnitt, der mit der 2. Klausur endete, griffen wir den Gedankengang, der schon früher zu der Frage nach der Steigung bei nicht linearem Funktionen geführt hatte, wieder auf, in dem das Gewichtsbeispiel erneut unter dem weitergehenden Gesichtspunkt betrachtet wurde.

Resümmee

Insgesamt dauerte der Teil des Unterrichts, der sich mit dem Grenzwertbegriff beschäftigte, länger, als ich ursprünglich vorgesehen hatte. Ich halte die Zeit aber nicht für verloren, da wichtige Grundlagen für die Analysis gelegt wurden, die aus der SI nicht in ausreichendem Maße vorhanden waren. Der Verzicht auf eine exakte Behandlung des Grenzwertes mit dem Lösen von Betragsungleichungen brachte Zeit für Diskussionen Grenzwerte und Dichtheit, die ich in früheren Durchgängen nicht hatte. Gleichzeitig habe ich den Eindruck, dass die Schülerinnen eine bessere Vorstellung vom Grenzwert haben, als das früher der Fall war, da jetzt nicht die algebraischen Probleme das eigentliche Verstehen überdeckten.  

Trotzdem muss ich sagen, dass die Aussage des Lehrplanes "ein anschaulich geprägter und nicht-formaler Grenzwertbegriff reicht an dieser Stelle völlig aus" zu optimistisch war. Dieser Grenzwertbegriff war in meiner Klasse zu Beginn der 11 nicht vorhanden und musste erst entwickelt werden. Vielleicht können wir das Problem aber auch dadurch lösen, dass wir in Zukunft an den entsprechenden Stellen in der Sekundarstufe I den Grenzwertbegriff stärker vorbereiten.

zurück zur Startseite