Eine Anwendungsaufgabe: Gewichtszunahme 

Bei diesem Aufgabenbeispiel handelt es sich um einen der gar nicht so seltenen Fälle, in denen eine Aufgabe sehr viel mehr an Möglichkeiten ergibt als eigentlich geplant war. Im Zusammenhang mit dem Thema "Modellierung durch Funktionen" bin ich auf ein Beispiel durch einen Studenten gestossen, das dazu geeignet ist, das Lesen des Graphen zu üben. Vorangegangen waren im Unterricht ähnliche qualitative Untersuchungen an Geschwindigkeitsgraphen und Füllgraphen.

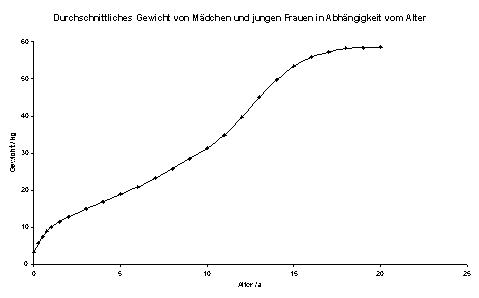
Vorgegeben war jetzt eine Tabelle zum Thema Gewicht und der zugehörige Funktionsgraph.

Tabelle:                                                  Graph

Zur Vorgehensweise im Unterricht: 

Zunächst wurden –wie von mir beabsichtigt- Informationen aus dem Graphen abgelesen:

• zunächst starke Zunahme des Gewichts, die sich dann verlangsamt;
• im Alter von 3 bis 6 Jahren gleichmäßige Gewichtszunahme;
• ebenso im Alter von 7 bis 10 Jahren und im Alter von 11 bis 14 Jahren, aber immer stärkere Zunahme;
• ab 14 Jahren immer geringer werdende Zunahme des Gewichts;
• ab 18 Jahren nahezu konstantes Gewicht.

Danach kam der Vorschlag, die Gewichtszunahme in den Abschnitten, in denen sie konstant ist, durch Zahlenwerte auszudrücken. Das führte uns zur impliziten Wiederholung der Steigung und zur Begriffsbildung "Gewichtszunahmerate" gemessen in kg/a. Damit waren wir mitten in der Koordinatengeometrie angelangt, mit der Zunahmerate am Beginn der Analysis.

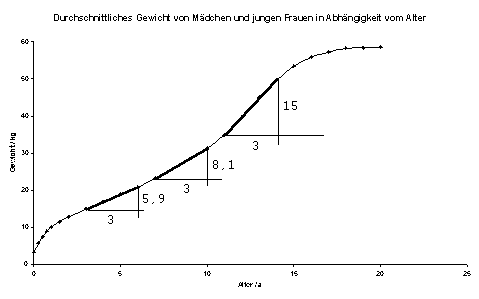
Schon bald stellten einzelne Schülerinnen die Frage, ob die Gewichtszunahmerate auch in nicht-linearen Abschnitten durch einen Zahlenwert beschreiben werden könnte. Wegen der anstehenden Klausur konnten wir erst nach einer längeren Unterbrechung diese Frage aufgreifen. Dazu musste zunächst für einen solchen Abschnitt eine Funktionsgleichung gefunden werden. Wir untersuchten den Zeitraum von 0 Jahren bis 2 Jahre. Der Verlauf des Graphen erinnerte die Schülerinnen an eine Wurzelfunktion. Der erste Ansatz berücksichtigte zwar den Anfangspunkt des Graphen, lieferte aber im weiteren Verlauf zu geringe Werte. Ein verbesserter Ansatz mit der Bedingung liefert , also . Mit dieser Funktion waren die Schülerinnen zufrieden, wenn auch die Werte im Intervall [0; 0,75] gegenüber den gegebenen Daten etwas zu hoch lagen.

Es war klar, dass die Zunahmerate zu jedem Zeitpunkt einen anderen Wert haben würde. Deshalb betrachteten wir zunächst den Zeitpunkt 1 a. Wie üblich wurden durchschnittliche Zunahmeraten zunächst auf konkreten Intervallen mit dem Endpunkt 1 gebildet. Es wurde vermutet, dass der Durchschnittswert um so näher an 0,5 liegen würde, je kleiner das Intervall war. Zur Bestätigung bildeten wir die Zunahmerate für die Intervalle und bestimmten den Grenzwert unter Verwendung der anschaulich klaren Grenzwertsätze.

An diesem Beispiel habe ich gesehen, dass die im Lehrplan geforderte implizite Wiederholung tatsächlich funktioniert und sich die Bereiche Koordinatengeometrie und Analysis gut vernetzen lassen. Der Forderung des Lehrplanes, sich auf ganz-rationale Funktionen zu beschränken, bin ich natürlich nicht gerecht geworden. Das nahm ich gerne in Kauf, denn der Glücksfall dieses recherchierte Datenmaterial war einfach zu reizvoll.

zurück