Aufgaben von Schülerinnen erstellt zur eigenen Vorbereitung auf die Klausur
Da uns kein Schulbuch zur Verfügung stand, stellte ich den Schülerinnen zur Vorbereitung auf die Klausur die Aufgabe, selbständig nach dem Muster der im Unterricht und in den Hausaufgaben behandelten Beispiele Übungsaufgaben für die Mitschülerinnen zu erstellen. Es sollten Aufgaben zum Themenbereich: Modellierung von Anwendungssituationen durch Funktionen und Koordinatengeometrie, gestellt werden Aus den mir eingereichten Beispielen habe ich hier eine Sammlung erstellt, die einen Eindruck von den Unterrichtsinhalten zu diesem Themenbereich vermittelt.. Es wird erkennbar, dass das Thema Modellierung ganz zwanglos in das Thema Koordinatengeometrie führte. Dabei ist anzumerken, dass zum Zeitpunkt der Klausur noch keine Parabeln behandelt worden waren und diese deshalb in den Aufgaben nicht vorkommen. Es stellte sich heraus, dass die von den Schülerinnen erfundenen Aufgaben teilweise erheblich komplexer waren, als die im Unterricht behandelten.
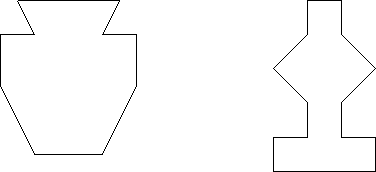
Aufgabe1 (von Andrea Huben und Britta Hülshorst)
Skizziere zu jedem Gefäß den Graphen der Wasserstandsfunktion bei konstanter Wasserzulaufrate.
a) b)
Aufgabe 2. (von Conny Sack):
Konstruiere eine mögliche Rennstrecke zum Geschwindigkeitsgraphen!
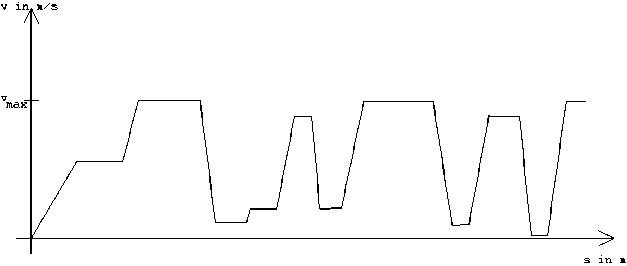
Aufgabe 3 (von Eva-Maria Hanschmann)
Zeichne eine Vase, die zu diesem Füllgraphen passt!
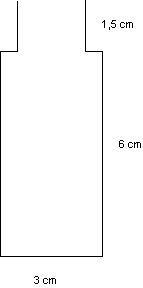
Aufgabe 4 (Nadine Gapp)
| Das Gefäß hat eine quadratische Querschnittsfläche. Es wird mit
einer konstanten Zulaufrate von
|
 |
Aufgabe 5 (von Juliane Welp):
Das Gefäß hat eine kreisförmige Querschnittsfläche. Die Grundfläche hat einen
Inhalt von 5 cm². Es wird mit konstanter Wasserzulaufrate von 
gefüllt. Die Füllung
des oberen Zylinders dauert 5 s.
|
|
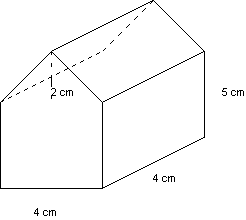
Aufgabe 6 (von Diana Klesen):
Das dargestellte Gefäß soll mit konstanter Zulaufrate von  gefüllt werden. a) Stelle den Graphen der Höhenfunktion und der Höhenanstiegsratenfunktion dar. b) Wie groß ist der Flächeninhalt einer der schrägen Flächen? c) Wie groß ist das Volumen des Gefäßes? d) Wie lange dauert der Füllvorgang? |
 |
Aufgabe 7 (von Dorothee Klocke):
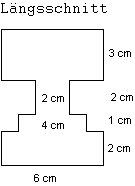
Die Darstellung zeigt einen Längsschnitt durch ein Gefäß. Das Gefäß
wird so gefüllt, dass das Wasser nach 10 s 2 cm hoch steht.
|
 |
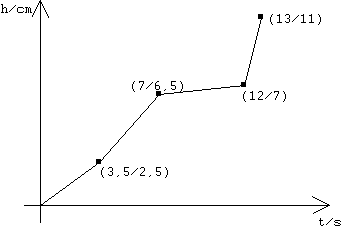
Aufgabe 8 (von Angela Orth)
Ein Gefäß wird mit konstanter Wasserzulaufrate von  gefüllt. Dargestellt ist die Füllgraph. Zeichne
einen maßstäblichen Längsschnitt durch das Gefäß, das einen runden Querschnitt hat. |
 |
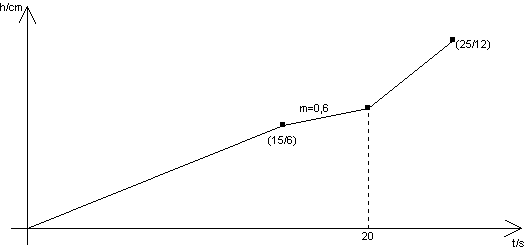
Aufgabe 9 (von Christina Weber).
Ein Gefäß mit kreisförmigem Querschnitt wird mit konstanter Zulaufrate von 
gefüllt. Zeichne einen
maßstäblichen Längsschnitt!
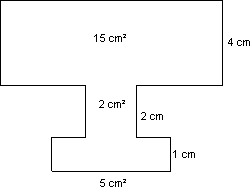
Aufgabe 10 (von Nadine Treptau):
Das dargestellte Gefäß soll so gefüllt werden, daß die
Höhenanstiegsrate in allen Abschnitten 
beträgt.
|
 |
gefüllt.