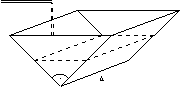
 |
Das abgebildete Gefäß soll mit Wasser gefüllt werden, so daß die Höhe des Wasserspiegels im Gefäß gleichmäßig ansteigt. |
Variante 1
Einstieg in die Differentialrechnung mit dem Begriff der Änderungsrate
Vorausgegangen sind Füllaufgaben. Dabei werden verschieden geformte Gefäße mit konstanter Zulaufrate gefüllt. Es wird jeweils die Funktion betrachtet, die den Zusammenhang zwischen der Zeit und der Höhe des Flüssigkeitsstandes im Gefäß angibt. Durch solche Aufgaben ist der Begriff der 'Rate' als Quotient aus zwei Größen den Schülerinnen bekannt.
Aufgabenstellung:
 |
Das abgebildete Gefäß soll mit Wasser gefüllt werden, so daß die Höhe des Wasserspiegels im Gefäß gleichmäßig ansteigt. |
Aus dem vorausgegangenen Unterricht wissen die Schülerinnen, daß bei konstanter Zulaufrate ein gleichmäßiges Ansteigen nur bei konstanter Querschnittsfläche des Gefäßes erfolgt. Daher ist unmittelbar klar, daß jetzt keine konstante Zulaufrate möglich ist. Die Zulaufrate muß deshalb durch eine Funktion beschrieben werden.
Qualitative Aussagen sind bereits möglich: Da das Gefäß nach oben breiter wird, müssen die Werte der Zulaufratenfunktion mit der Zeit ansteigen.
Zunächst wird diskutiert, welche Zahlenwerte für eine quantitative Auswertung
erforderlich sind. Die Tiefe des Gefäßes ist dabei sofort einsichtig. Ein
gleichmäßiger Höhenanstieg bedeutet, daß ![]() . Also ist a vorzugeben. Für die Einführung empfiehlt es sich, mit
konkreten Werten zu arbeiten, z. B.
. Also ist a vorzugeben. Für die Einführung empfiehlt es sich, mit
konkreten Werten zu arbeiten, z. B. ![]() und
und ![]() . Häufig wird von den
Schülerinnen auch vorgeschlagen, die Höhe des Gefäßes vorzugeben. Manchmal erkennen
sie erst zu einem späteren Zeitpunkt, daß diese Angabe für die Bestimmung der
Zulaufrate keine Rolle spielt.
. Häufig wird von den
Schülerinnen auch vorgeschlagen, die Höhe des Gefäßes vorzugeben. Manchmal erkennen
sie erst zu einem späteren Zeitpunkt, daß diese Angabe für die Bestimmung der
Zulaufrate keine Rolle spielt.
Da es in der Regel schwierig ist, unmittelbar einen Funktionsterm zu bestimmen, werden zunächst einzelne konkrete Funktionswerte ermittelt.
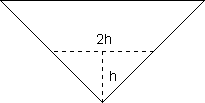 |
Betrachtet werde der Zeitpunkt 2 min. Zu diesem Zeitpunkt muß das Wasser
10 cm hoch stehen. die Zulaufrate wird in |
Bisher kam im Unterricht immer die Idee auf, das Volumen zu einem späteren Zeitpunkt zu berechnen, um daraus Informationen über die Zulaufrate zu gewinnen.
Eine mögliche Rechnung ist ![]() .
. ![]() , somit müssen von der 2. zur 3. Minute
, somit müssen von der 2. zur 3. Minute ![]() zufließen. Die Zulaufrate beträgt
zufließen. Die Zulaufrate beträgt ![]() .
.
Bei der Diskussion dieses Ergebnisses (eventuell ist ein Hinweis auf die über eine Minute konstante Zulaufrate erforderlich) erkennen die Schülerinnen, daß es sich bei dem ermittelten Wert nur um einen Durchschnittswert für das Zeitintervall [2;3] handelt. Der tatsächlich gesuchte Wert muß kleiner sein, da sich das Gefäß nach oben öffnet.
Durch Verkleinerung des Zeitintervalls erhält man Durchschnittswerte, die besser mit dem gesuchten Wert übereinstimmen. Nachdem einige konkrete, immer kleinere Intervalle betrachtet wurden, kommen die Schülerinnen zu der Erkenntnis, daß sie eine Folge von durchschnittlichen Zulaufraten betrachten, deren Grenzwert die gesuchte Zulaufrate ist.
Betrachtet wird das Intervall ![]() .
.
Die durchschnittliche Zulaufrate beträgt 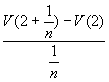 . Nach Vereinfachung des Terms wird der Grenzwert gebildet.
. Nach Vereinfachung des Terms wird der Grenzwert gebildet.
Nachdem einige derartige Berechnungen durchgeführt wurden, stellt sich die Frage nach einer graphischen Veranschaulichung. Bekannt ist, daß sich Funktionen durch einen Graphen veranschaulichen lassen.
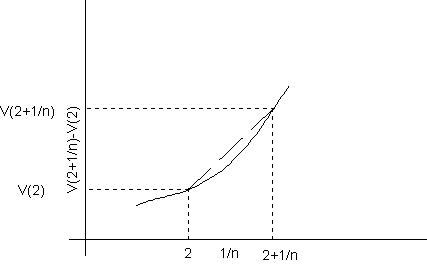 |
Alle Teile der Berechnung werden in den Graphen eingetragen. Der Quotient
schließlich erinnert die Schülerinnen an die Steigung einer Geraden. Auch diese Gerade
wird eingetragen. Damit erhält man die Steigung der Sekante als Veranschaulichung für
die durchschnittliche Änderungsrate in einem Intervall. Bei der Grenzwertbildung rücken die Punkte auf dem Graphen, durch die die Sekante verläuft immer näher zusammen, so daß die Änderungsrate durch die Steigung der Tangente veranschaulicht wird. |
Einstieg in die Differentialrechnung