Aufgaben zu Durchschnitt, Standardabweichung und speziell zur Normalverteilung

 

Aufgabe 1: 

  1. Weisen Sie nach, dass die Funktion mit der Gleichung 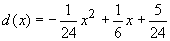im Intervall 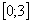eine Dichtefunktion ist.
  2. Berechnen Sie die Wahrscheinlichkeit für ein Ergebnis im Intervall .
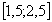  3. Bestimmen Sie den Durchschnittswert und die Standardabweichung.
  4. Begründen Sie, warum der Durchschnitt in diesem Fall mit Hilfe eines Integrals berechnet werden muss.

Lösung: 

 

Aufgabe 2:

Gegeben ist eine Schar von Funktionen im Intervall 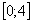durch .

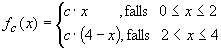  1. Skizzieren Sie den Funktionsgraphen.
  2. Bestimmen Sie den Wert für den Parameter c so, dass es sich um eine Dichtefunktion handelt.
  3. Begründen Sie, warum man in diesem Fall von der "Dreiecksverteilung" spricht.
  4. Bestimmen Sie den Mittelwert und die Standardabweichung.
  5. Berechnen Sie die Wahrscheinlichkeit für ein Ergebnis zwischen 1,9 und 2,3.

 

 

Vorbemerkung: Die Aufgaben zur Normalverteilung werden wegen der Integrale sinnvollerweise mit Hilfe eines Computeralgebrasystems bearbeitet.

 

Aufgabe 3:

Bei der Befüllung von Zuckertüten durch eine Maschine ist das Gewicht normalverteilt mit Mittelwert 1000 g und Standardabweichung 6 g.

  1. Wie viele Zuckertüten enthalten weniger als 995 g?
  2. Der Produzent möchte eine Garantie geben, so dass eine Tüte mit zu geringer Füllung umgetauscht werden kann. Welche Mindestfüllmenge sollte er garantieren, wenn er, besonders kritische Kunden vorausgesetzt, höchstens ein Prozent an Reklamationen haben will?

 Lösung

 

Aufgabe 4:

Eine Maschine produziert Nägel. Für die Länge ergibt sich ein Durchschnittswert von 25 mm und eine Standardabweichung von 0,6 mm.

  1. Mit welcher Wahrscheinlichkeit werden Nägel produziert, deren Länge um weniger als 1 mm vom Durchschnittswert abweicht?
  2. Sie wollen als Produzent Ihren Kunden eine Garantie bezüglich der Länge der Nägel geben. Sie möchten allerdings höchstens 1% Reklamationen haben. Welche Garantie würden Sie geben? Denken Sie daran, dass sowohl zu kurze als auch zu lange Nägel unbrauchbar sind.
  3. Sie wollen Ihre Garantiezusage nicht verändern, aber nur noch höchsten 0,5 % Reklamationen haben. Dazu planen Sie den Kauf einer besseren Maschine. Welche Standardabweichung sollte diese Maschine haben?

 Lösung

 

Weitere Aufgaben zur Normalverteilung sind in großer Anzahl in den gängigen Schulbüchern zu finden.

 

zurück