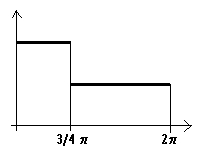
| Aufgabe 1: Gegeben ist die Dichtefunktion eines Glücksrads. Dabei sind die Funktionswerte am Anfang doppelt so hoch wie am Ende. |
 |
Aufgaben zu stückweise konstanten Dichtefunktionen:
| Aufgabe 1: Gegeben ist die Dichtefunktion eines Glücksrads. Dabei sind die Funktionswerte am Anfang doppelt so hoch wie am Ende. |
 |
Aufgabe 2:
Durch 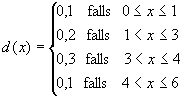 ist im
Intervall
ist im
Intervall ![]() eine Funktion gegeben.
eine Funktion gegeben.
Aufgabe 3:
Bestimmen Sie die Gleichung der Dichtefunktion für ein nicht manipuliertes Glücksrad.