Klausuraufgaben zur Integralrechung
1.
- Erläutern Sie am Beispiel
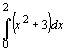 , wie man ein Integral
berechnet. Stellen Sie die wichtigen Grundideen dar.
, wie man ein Integral
berechnet. Stellen Sie die wichtigen Grundideen dar.
- Veranschaulichen Sie Ihre Erläuterung durch eine Skizze.
- Nehmen Sie an,
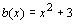 wäre eine Breitenfunktion. Was wird dann
mit Hilfe des Integrals berechnet? Begründen Sie Ihre Antwort.
wäre eine Breitenfunktion. Was wird dann
mit Hilfe des Integrals berechnet? Begründen Sie Ihre Antwort.
- Nehmen Sie an,
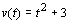 wäre eine Geschwindigkeitsfunktion. Was
wird dann mit Hilfe des Integrals berechnet? Begründen Sie Ihre Antwort.
wäre eine Geschwindigkeitsfunktion. Was
wird dann mit Hilfe des Integrals berechnet? Begründen Sie Ihre Antwort.
2. Gegeben ist eine Geschwindigkeitsfunktion durch 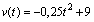 .
Dabei wird v in m/s und t in s angegeben. Die Bewegung beginnt zum Zeitpunkt 0 s und endet
beim Stillstand des Fahrzeugs.
.
Dabei wird v in m/s und t in s angegeben. Die Bewegung beginnt zum Zeitpunkt 0 s und endet
beim Stillstand des Fahrzeugs.
- Wie groß ist die Geschwindigkeit zu Beginn?
- Zu welchen Zeitpunkt steht das Fahrzeug?
- Wie lang ist der Bremsweg (bis zum Stillstand des Fahrzeugs)?
- Begründen Sie, daß Sie zur Lösung der Aufgabe die Integralrechnung verwenden mußten.
- Formulieren Sie eine Aufgabe, in der es ebenfalls um die Berechnung eines Weges mit
Hilfe der Geschwindigkeit geht, die aber ohne Integralrechnung zu lösen ist.
3. Gegeben ist eine Geschwindigkeitsfunktion durch 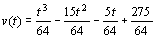 . Dabei wird v in m/s und t in s angegeben. Die Bewegung beginnt
zum Zeitpunkt 0 s und endet beim Stillstand des Fahrzeugs.
. Dabei wird v in m/s und t in s angegeben. Die Bewegung beginnt
zum Zeitpunkt 0 s und endet beim Stillstand des Fahrzeugs.
- Wie groß ist die Geschwindigkeit zu Beginn?
- Zu welchen Zeitpunkt steht das Fahrzeug?
- Wie lang ist der Bremsweg (bis zum Stillstand des Fahrzeugs)?
- Begründen Sie, daß Sie zur Lösung der Aufgabe die Integralrechnung verwenden mußten.
- Formulieren Sie eine Aufgabe, in der es ebenfalls um die Berechnung eines Weges mit
Hilfe der Geschwindigkeit geht, die aber ohne Integralrechnung zu lösen ist.
4. Gegeben ist die Zulaufratenfunktion für ein Wasserbecken durch 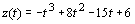 im Intervall [0; 6]. Dabei ist t in
Stunden in z in m³/h gemessen. Negative Werte der Zulaufratenfunktion bedeuten, dass
Wasser abläuft.
im Intervall [0; 6]. Dabei ist t in
Stunden in z in m³/h gemessen. Negative Werte der Zulaufratenfunktion bedeuten, dass
Wasser abläuft.
- Bestimmen Sie die Zeitintervalle, in den Wasser zuläuft und die Intervalle, in denen
Wasser abläuft.
- Wie viel Wasser ist bis zum Ende der ersten Zulaufphase zugelaufen?
- Zu welchem Zeitpunkt ist während der Ablaufphase der Anfangswasserstand wieder
erreicht?
- Zu welchem Zeitpunkt ist das Becken am stärksten gefüllt?
- Zu welchem Zeitpunkt liegt die größte Zulaufrate vor?
- Zu welchem Zeitpunkt liegt die größte Ablaufrate vor?
- Zu welchem Zeitpunkt liegt die maximale Änderung der Zulaufrate vor?
- Nehmen Sie an, es würde sich bei der Funktion um eine Geschwindigkeitsfunktion handeln.
Geben Sie zu jedem der Aufgabenteile a) bis h) an, was Sie dann ausgerechnet hätten.
5. Wenn mit einem Computer Daten aus dem Internet geladen werden, kann man auf dem
Bildschirm ständig die Übertragungsrate ablesen. Der Wert der Übertragungsrate ist in
der Regel nicht konstant. Die Übertragungsrate wird in KB/s gemessen. KB ist dabei die
Einheit zur Messung der Datenmenge. Grob gerechnet bedeutet 1 KB eine Datenmenge von 1000
Buchstaben.
Bei einem Ladevorgang ergab sich eine Übertragungsratenfunktion mit der Gleichung 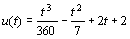 . Der Übertragungsvorgang dauerte 30 s.
. Der Übertragungsvorgang dauerte 30 s.
- Wie groß war die gesamte übertragene Datenmenge?
- Zu welchem Zeitpunkt war die Hälfte der Datenmenge übertragen?
- Zu welchem Zeitpunkt war die Rate maximal, wann war sie minimal? Wie groß waren die
Extrtemwerte?
- Zu welchem Zeitpunkt ist die Rate besonders stark abgesunken?
- Wie lange hätte der Übertragungsvorgang gedauert, wenn der Anfangswert der
Übertragungsrate die ganze Zeit über beibehalten worden wäre?
- Angenommen, es hätte sich bei der Funktion um eine Zulaufratenfunktion für ein
Wasserbecken gehandelt. Geben Sie zu jedem Aufgabenteil an, was dann mit der jeweiligen
Rechnung bestimmt worden wäre.
6. Gegeben ist ein gedrechselter Körper. Sein Radius wird durch die Funktion mit der
Gleichung 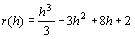 gegeben. Dabei werden r
und h in cm gemessen. Der Körper hat eine Höhe von 5,5 cm.
gegeben. Dabei werden r
und h in cm gemessen. Der Körper hat eine Höhe von 5,5 cm.
- Berechnen Sie das Volumen des Körpers.
- Bestimmen Sie den Radius im unteren und im oberen Punkt des Körpers.
- Untersuchen Sie, wo der Körper besonders breit und wo er besonders schmal ist.
- Skizzieren Sie den Körper.
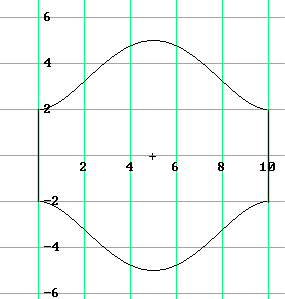
| 7. Ein Raum in einem Barockschloß hat den dargestellten Grundriß. Bestimmen Sie
den Flächeninhalt des Raumes. |
 |
8. Gegeben ist ein Körper mit kreisförmigen Querschnittsflächen. Der Körper ist 4
cm hoch. Zu verschiedenen Höhen wurde jeweils der Durchmesser des Körpers gemessen:
- Geben Sie eine Funktion an, die zu den jeweiligen Höhen gerade die gemessenen
Durchmesser liefert.
- Wo ist der Körper am schmalsten, wo am breitesten?
- Skizzieren Sie den Körper.
- Berechnen Sie das Volumen des Körpers.
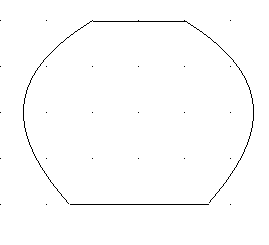
| 9. Gegeben ist ein Körper mit kreisförmigen Querschnitten.
Der Längsschnitt ist abgebildet. Die Rasterpunkte haben einen Abstand von jeweils 1 cm.
Bestimmen Sie das Volumen des Körpers. |
 |
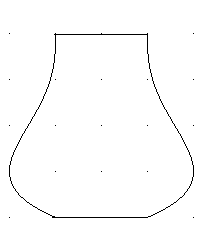
| 10. Gegeben ist ein Körper mit kreisförmigen Querschnitten.
Der Längsschnitt ist abgebildet. Die Rasterpunkte haben einen Abstand von jeweils 1 cm.
Bestimmen Sie das Volumen des Körpers.
Kontrollieren Sie, durch eine graphische Darstellung, ob Ihr Körper die gleichen
Eigenschaften hat wie der dargestellte. |
 |
Startseite
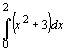 , wie man ein Integral
berechnet. Stellen Sie die wichtigen Grundideen dar.
, wie man ein Integral
berechnet. Stellen Sie die wichtigen Grundideen dar.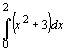 , wie man ein Integral
berechnet. Stellen Sie die wichtigen Grundideen dar.
, wie man ein Integral
berechnet. Stellen Sie die wichtigen Grundideen dar.![]() .
Dabei wird v in m/s und t in s angegeben. Die Bewegung beginnt zum Zeitpunkt 0 s und endet
beim Stillstand des Fahrzeugs.
.
Dabei wird v in m/s und t in s angegeben. Die Bewegung beginnt zum Zeitpunkt 0 s und endet
beim Stillstand des Fahrzeugs.
![]() . Dabei wird v in m/s und t in s angegeben. Die Bewegung beginnt
zum Zeitpunkt 0 s und endet beim Stillstand des Fahrzeugs.
. Dabei wird v in m/s und t in s angegeben. Die Bewegung beginnt
zum Zeitpunkt 0 s und endet beim Stillstand des Fahrzeugs.
![]() im Intervall [0; 6]. Dabei ist t in
Stunden in z in m³/h gemessen. Negative Werte der Zulaufratenfunktion bedeuten, dass
Wasser abläuft.
im Intervall [0; 6]. Dabei ist t in
Stunden in z in m³/h gemessen. Negative Werte der Zulaufratenfunktion bedeuten, dass
Wasser abläuft.
![]() . Der Übertragungsvorgang dauerte 30 s.
. Der Übertragungsvorgang dauerte 30 s.
![]() gegeben. Dabei werden r
und h in cm gemessen. Der Körper hat eine Höhe von 5,5 cm.
gegeben. Dabei werden r
und h in cm gemessen. Der Körper hat eine Höhe von 5,5 cm.


