Klausuraufgaben zur Differentialrechnung
Im Folgenden werden Aufgaben angeboten, die in Klausuren verwendet wurden. Bei einigen
der Aufgaben war die Verwendung eines Computer-Algebra-Systems möglich. Die Aufgaben
wurden sowohl in Grund- als auch in Leistungskursen eingesetzt.
1. Die Volumenfunktion in einem Gefäß ist durch die Gleichung 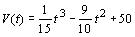 im Intervall [0;18] gegeben.
im Intervall [0;18] gegeben.
Der Graph ist auf dem beiliegenden Blatt abgedruckt.
- Beschreiben Sie in Worten, was Sie aus dem Graphen ablesen können.
- Wieviel von dem Volumen wird im Intervall [0;10] verbraucht? Wie groß ist die
durchschnittliche Verbrauchsrate in diesem Intervall?
- Zu welchem Zeitpunkt ist die Hälfte des Anfangsvolumens im Gefäß?
- Gibt es Zeitpunkte, zu denen nichts verbraucht wird?
- Zu welchem Zeitpunkt im Intervall [0;10] ist der Verbrauch maximal? Wie groß ist der
maximale Verbrauch?
- Zu welchem Zeitpunkt im Intervall [0;10] ist der Verbrauch minimal? Wie groß ist der
minimale Verbrauch?
- Von welchem Zeitpunkt an wird das Gefäß wieder gefüllt?
- Wann ist die Anfangsfüllung wieder erreicht?
2. Gegeben ist eine Volumenfunktion durch einen Term V(t). Schreiben Sie jeweils auf,
zu welcher Fragestellung der Rechenansatz paßt:
- V(17)
- V(t) = 5,3
- V(12) – V(3)
- V‘(t) = 0
- V‘(5)
3. Die Füllmenge in einem Vorratsbehälter ist durch die Funktion mit der Gleichung 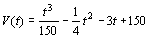 gegeben. Dabei ist V in m³ und t in
Stunden gemessen. Betrachtet wird der Ablauf eines Tages, also t liegt zwischen 0 und 24.
gegeben. Dabei ist V in m³ und t in
Stunden gemessen. Betrachtet wird der Ablauf eines Tages, also t liegt zwischen 0 und 24.
- Wie groß ist der Verbrauch im Laufe des Tages?
- Ist der Vorratsbehälter im Laufe des Tages irgendwann leer?
- Wann ist die Hälfte der Anfangsmenge im Behälter?
- Wie groß ist die durchschnittliche Verbrauchsrate während des Tages?
- Zu welchem Zeitpunkt ist der Verbrauch maximal?
- Zu welchem Zeitpunkt ist der Verbrauch minimal?
- Wie groß ist der minimale bzw. maximale Verbrauch?
4. Durch die Funktion mit der Gleichung h(t)=-0,004t3+0,05t2+t
wird der Wasserstand in einem Regenmesser angegeben. Dabei ist t in Stunden und h in mm
gemessen. Betrachtet wird das Zeitintervall [0;12].
- Wie viel Regen ist in der gesamten Zeit gefallen?
- Ist in der ersten Hälfte des Intervalls mehr Regen gefallen oder in der zweiten?
- Beschrieben Sie, wie Sie die Regenheftigkeit mathematisch ausdrücken können.
- Hat es zum Zeitpunkt 2 Stunden oder zum Zeitpunkt 4 Stunden stärker geregnet?
- Wann hat es im Laufe des Zeitintervalls am stärksten geregnet? Wann hat es am wenigsten
geregnet?
Geben Sie zu jedem Aufgabenteil eine Begründung.
5. Durch die Gleichung v(t) = t3 – 9t2 + 27 t + 4 ist eine
Geschwindigkeitsfunktion im Intervall [0;5] gegeben. Dabei wird t in s und v in km/h
gemessen.
- Wie groß ist die Geschwindigkeit nach 2 Sekunden?
- Zu welchem Zeitpunkt ist die Geschwindigkeit maximal? Zu welchem Zeitpunkt ist sie
minimal? Wie groß sind maximale bzw. minimale Geschwindigkeit?
- Zu welchem Zeitpunkt ist die Beschleunigung maximal? Zu welchem Zeitpunkt ist sie
minimal? Wie groß sind maximale bzw. minimale Beschleunigung?
6. Durch die Gleichung v(t) = t3 – 12t2 + 48 t + 3 ist eine
Geschwindigkeitsfunktion im Intervall [0;5] gegeben. Dabei wird t in s und v in km/h
gemessen.
- Wie groß ist die Geschwindigkeit nach 3 Sekunden?
- Zu welchem Zeitpunkt ist die Geschwindigkeit maximal? Zu welchem Zeitpunkt ist sie
minimal? Wie groß sind maximale bzw. minimale Geschwindigkeit?
- Zu welchem Zeitpunkt ist die Beschleunigung maximal? Zu welchem Zeitpunkt ist sie
minimal? Wie groß sind maximale bzw. minimale Beschleunigung?
Startseite
![]() im Intervall [0;18] gegeben.
im Intervall [0;18] gegeben.![]() gegeben. Dabei ist V in m³ und t in
Stunden gemessen. Betrachtet wird der Ablauf eines Tages, also t liegt zwischen 0 und 24.
gegeben. Dabei ist V in m³ und t in
Stunden gemessen. Betrachtet wird der Ablauf eines Tages, also t liegt zwischen 0 und 24.