und
. Mit Hilfe der Normalverteilungsfunktion
mit diesem beiden Parametern wird die zu erwartende Anzahl der Messwerte berechnet. Stunde 19 ; Doppelstunde 20/21 : Anpassen einer Normalverteilung an empirische Daten
Aufgabe (nach bsv, S. 185)
Die Dichte einer Flüssigkeit wurde 100-mal gemessen. Es ergab sich folgende Verteilung der Messwerte:
Dichte x in g/cm³ Anzahl der Messwerte x £ 4,96 3
4,96 < x £ 4,98 10
4,98 < x £ 5,00 23
5,00 < x £ 5,02 31
5,02 < x £ 5,04 22
5,04 < x £ 5,06 9
5,06 < x 2
Überprüfen Sie, ob die Werte sich durch die Dichtefunktion einer Normalverteilung beschreiben lassen.
Zur Lösung wird zunächst der Mittelwert und die Standardabweichung der Messwerte bestimmt. Da die Anzahl der Messwerte jeweils für ein ganzes Intervall angegeben ist, wird für die Berechnung der mittlere Wert des jeweiligen Intervalls gewählt:
Dichte x in g/cm³
Anzahl der Messwerte 4,95
3
4,97
10
4,99
23
5,01
31
5,03
22
5,05
9
5,07
2
Es bietet sich an, die rechenintensive Auswertung mit Hilfe einer Tabellenkalkulation
zu machen. Es ergeben sich die Werte und
. Mit Hilfe der Normalverteilungsfunktion
mit diesem beiden Parametern wird die zu erwartende Anzahl der Messwerte berechnet.
Als Beispiel wird ein Intervall betrachte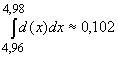t:
, also sind von den 100 Messwerten 10 in diesem Intervall zu erwarten,
was mit dem empirischen Ergebnis übereinstimmt.
Entsprechend lässt sich das für die übrigen Intervalle überprüfen. Das Ergebnis ist
bei diesem Beispiel eine sehr gute Übereinstimmung zwischen der Rechnung und den
empirischen Werten, so dass damit bestätigt wurde, dass sich die Messwerte durch die
Dichtefunktion einer Normalverteilung beschreiben lassen.
In einer Excel-Tabelle läßt sich auch eine Spalte für die Berechnung vorsehen, so dass die Bestimmung der Parameter und die Prüfung der Übereinstimmung zusammen durchgeführt werden können.