Stunde 13 ; Doppelstunde 14/15: Standardabweichung
Ausgehend von der Standardabweichung bei endlich vielen möglichen Werten wird die
Berechnungsformel für den stetigen Fall hergeleitet.
Es gilt 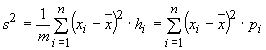 , wobei die möglichen Werte
, wobei die möglichen Werte 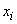 jeweils die Häufigkeit
jeweils die Häufigkeit 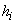 haben und insgesamt
haben und insgesamt 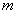 Ergebnisse vorliegen.
Ergebnisse vorliegen.
Wählt man auch hier als Zwischenschritt die stückweise konstanten Dichtefunktionen, kann
nicht so anschaulich wie beim Durchschnittswert argumentiert werden. Wegen des Quadrates
haben innerhalb eines Intervalls die Werte, die weiter vom Durchschnitt entfernt sind, ein
größeres Gewicht. Führt man hier die stückweise konstanten Dichtefunktionen auf einen
endlichen Fall zurück, wird das 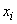 in der
Regel nicht der mittlere Wert des Intervalls sein, sondern irgendein Wert im Intervall.
in der
Regel nicht der mittlere Wert des Intervalls sein, sondern irgendein Wert im Intervall.
Diese Schwierigkeit, die natürlich nur ein Problem des exakten Hinschreibens ist, kann
man umgehen, wenn die Analogie zur Durchschnittsberechnung betrachtet wird:
| Durchschnitt: |
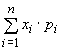 führt auf führt auf 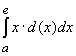 ; ; |
| Standardabweichung: |
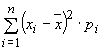 führt auf führt auf 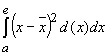 . . |
zurück
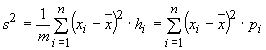 , wobei die möglichen Werte
, wobei die möglichen Werte 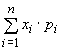 führt auf
führt auf 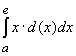 ;
;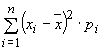 führt auf
führt auf 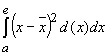 .
.