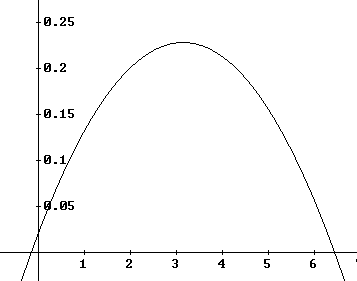
| Betrache die Funktion mit der Gleichung Es könnte sich um eine Dichtefunktion handeln, wenn die Wahrscheinlichkeit für ein Ergebnis irgendwo im Intervall den Wert 1 hätte. |
 |
Doppelstunde 7/8: Stetige Dichtefunktionen
| Betrache die Funktion mit der Gleichung Es könnte sich um eine Dichtefunktion handeln, wenn die Wahrscheinlichkeit für ein Ergebnis irgendwo im Intervall den Wert 1 hätte. |
 |
Zur Berechnung von Wahrscheinlichkeiten kann in diesem Fall nicht mehr die
Multiplikation bzw. die Addition von Produkten verwendet werden, da die Funktion nicht
stückweise konstant ist. Da die Integralrechnung anzuwenden ist, wenn bei einem Produkt
einer der Faktoren nicht konstant ist, gilt allgemein 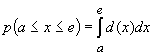 . Speziell ist
. Speziell ist 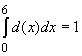 , also
handelt es sich um eine Dichtefunktion.
, also
handelt es sich um eine Dichtefunktion.
Es kann definiert werden:
Eine Funktion f ist genau dann eine Dichtefunktion in einem Intervall
, wenn es im Intervall keine negativen Funktionswerte gibt und
.