Doppelstunde 2/3; Dichtefunktionen

In dieser Stunde wurde ein selbst geschriebenes Programm verwendet. Das Programm simuliert ein Glücksrad.  

Der Umgang mit dem Programm unter Benutzung der Glücksradgraphik zeigt sehr schnell, dass in diesem Fall das Spiel für den Spieler absolut unfair ist. Konkret bedeutet es, dass jetzt bei unendlich vielen möglichen Ergebnissen der Begriff "Wahrscheinlichkeit für ein Ergebnis" keinen Sinn macht.

Eine Strategie zur Untersuchung des Glücksrades kann lauten:

• Es müssen viele Experimente durchgeführt werden.
• Das Glücksrad wird in Winkelintervalle eingeteilt, und es wird registriert, in welchem Intervall das Ergebnis des Experimentes liegt.
• Die relativen Häufigkeiten werden in einem Säulendiagramm dargestellt.

Die Durchführung vieler Simulationen zeigt bei der voreingestellten Intervallzahl von 10 einen hohen Wert im ersten Intervall, einen mittleren im zweiten und etwa gleich niedrige Werte in den restlichen Intervallen. Daraus kann gefolgert werden, dass im Intervall eine versteckte Bremse im Glücksrad eingebaut ist.

Veränderungen der Intervallzahlen führt zu den Erkenntnissen:

• je mehr Intervalle, desto niedriger die Werte für die relativen Häufigkeiten;
• Lage der Bremse im Intervall

.

Der spielerische Umgang mit der Option "Dichte" führt zu den Erkenntnissen:

• Die Funktionswerte bleiben unabhängig von der Intervallzahl in der gleichen Größenordnung.
• Je mehr Intervall verwendet werden, desto unregelmäßiger wird der Treppengraph.
• Je mehr Experimente gemacht wurden, desto regelmäßiger wird der Treppengraph.
• Bei sehr vielen (unendlich vielen) Experimenten ist die folgende Graph zu erwarten:
  
  

Damit ist plausibel gemacht, dass die Dichte wohl ein gut geeignetes Hilfsmittel ist, um das Verhalten des manipulierten Glücksrades zu beschreiben. Es ist aber noch nicht klar, was das Programm eigentlich macht, wenn die Option "Dichte" gewählt wurde. Ein Vergleich mit anderen Dichten (Bevölkerungsdichte, Dichte eines Stoffes, ...) legt die Vermutung nahe, dass in diesem Fall die Dichte der Quotient aus der relativen Häufigkeit und der Länge des Intervalls ist. Tatsächlich führt das Programm diese Berechnung durch.

Die Unabhängigkeit der Dichtewerte von der Zahl der Intervalle läßt sich leicht begründen:

Da die Dichtefunktion bisher nur durch den Graphen gegeben ist, soll auch ein Funktionsterm ermittelt werden.
Aus dem Graphen ist zu entnehmen, dass die Dichte am Anfang etwa doppelt so hoch ist wie am Ende.
Sei d der Funktionswert am Ende. Die Wahrscheinlichkeit, dass der Zeiger irgendwo auf dem Rad anhält ist 1. Aus der Definition der Dichte folgt, dass die Wahrscheinlichkeit durch Multiplikation der Dichte mit der Länge des Intervalls berechnet wird.
Da sich der Dichtewert zwischendurch ändert, sind zwei Produkte zu bilden und zu addieren: .

Also ist         .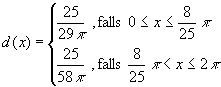

Mit Hilfe des Funktionsterms lassen sich nun Wahrscheinlichkeiten berechnen:

zurück